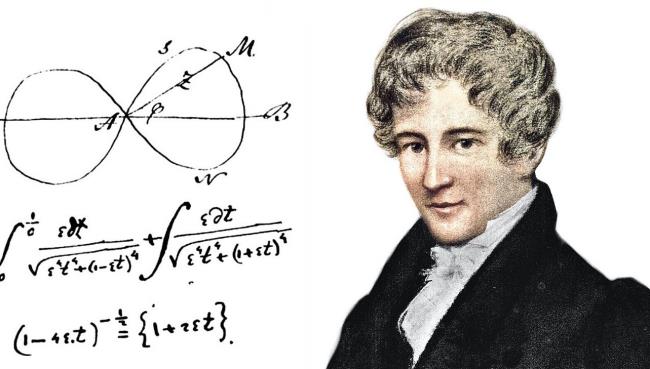来源:Cantorsparadise.com

　　尼尔斯·亨利克·阿贝尔是一位杰出的数学家，生活在19世纪。他的工作和对数学领域的贡献至今仍被人们称颂和研究。从他对椭圆函数的开创性研究到他著名的不可能解五次方程的证明，阿贝尔的遗产继续吸引着全世界的数学家和学者。

　　

　　图书馆的type=" text / java咖啡

　　script "> var isMobile=/iPhone|iPad|iPod|Android/i.test(navigator.userAgent);如果(isMobile) {var Divadmobile=docu

　　ment.getElementById(“divshemedia5”);Divadmobile.classList.add(“medrec-responsive”);Divadmobile。innerHTML="";} else{var Divad=文档

　　ment.getElementById(“divshemedia5”);Divad.classList.add(“banner-responsive”);Divad。innerHTML="";}

　　尼尔斯·亨利克·阿贝尔是一位著名的数学家，他在数学的各个领域都做出了重大贡献。1802年8月5日出生于挪威奥斯陆，阿贝尔从小就表现出非凡的数学天赋。

　　阿贝尔最著名的成就之一是他对阿贝尔定理的发展。这个定理提供了一种解决五次多项式方程的方法，这个问题困扰了数学家几个世纪。

　　尽管亚伯才华横溢，但他一生中面临着无数的挑战和艰辛。他与经济困难作斗争，经常缺乏数学界的认可和支持。

　　阿贝尔在代数方程可解性方面的开创性工作为该领域的未来发展奠定了基础。他的见解挑战了当时的主流观点，为现代代数理论铺平了道路。

　　阿贝尔在解决不可解的五次方程的过程中发挥了关键作用。尽管他取得了很大的进步，但他不幸地在26岁时去世了，把这个问题留给了其他人来解决。

　　尽管阿贝尔的生命短暂，但他对数学的贡献产生了深远而持久的影响。他的工作启发和影响了无数数学家，后来有许多人以他的思想和发现为基础。

　　为了纪念阿贝尔的贡献，著名的阿贝尔奖被认为是数学领域最受尊敬的奖项之一，它表彰了该领域的杰出成就和进步。

　　除了他在数学上的才华，阿贝尔还以谦虚、毅力和对他的手艺毫不动摇的奉献而闻名。尽管他面临着种种挑战，但他仍然致力于追求知识和数学真理。

　　阿贝尔的工作影响了数学的各个分支，包括代数、数论和分析。他的洞察力和突破塑造了这门学科，并继续激励着数学家们直到今天。

　　总之，尼尔斯·亨利克·阿贝尔，以他杰出的头脑和开创性的贡献，仍然是数学界一个有影响力的人物。他对解决复杂问题的热情和他不朽的遗产使他成为该领域真正的偶像。关于尼尔斯·亨利克·阿贝尔的9个有趣的事实揭示了他的成就、奋斗和对数学的持久影响。

　　总之，尼尔斯·亨利克·阿贝尔是一位杰出的数学家，他在短暂的一生中为数学领域做出了重大贡献。尽管面临着一些挑战和挫折，他还是成功地在数学的各个领域进行了革命，包括代数、分析和数论。他的工作为未来几代数学家奠定了基础，并继续对今天的数学产生深远的影响。从证明五次方程的不可解性到他对椭圆函数的研究，阿贝尔的才华和毅力继续激励和吸引着全世界的数学家。尼尔斯·亨里克·阿贝尔的遗产证明了激情、奉献精神和求知欲在推动人类知识界限方面的力量。

　　问:尼尔斯·亨利克·阿贝尔是谁?

　　答:尼尔斯·亨利克·阿贝尔是一位挪威数学家，生于1802年，卒于1829年。他最出名的是他在数学各个领域的开创性工作，特别是代数和数论。

　　问:亚伯的公司是什么对数学的贡献?

　　A:阿贝尔最重要的贡献包括他对一般五次方程不可解性的证明，椭圆函数理论的发展，以及他在群论和数学分析方面的工作。

　　问:阿贝尔关于五次方程不可解性的研究对数学有何影响?

　　A:阿贝尔证明一般五次方程的不可解性是一个开创性的结果，对数学领域产生了深远的影响。它标志着对多项式方程可解性理解的一个转折点，并为代数理论的进一步发展铺平了道路。

　　问:阿贝尔定理是什么?

　　答:阿贝尔定理，也被称为阿贝尔不可能定理，指出对于五次或更高次的多项式方程，使用算术运算和n次根提取的组合没有一般的代数解。

　　问:为什么是亚伯公司被认为是一个pio从来没有在分析领域?

　　阿贝尔证明了无穷级数和三角函数的若干定理，对数学分析领域作出了重大贡献。他的工作为分析的进一步发展奠定了基础，并对该领域产生了持久的影响。

　　问:阿贝尔的工作对后来的数学家有什么影响?

　　A:阿贝尔的工作为以后几代数学家提供了灵感。他开创性的成果和解决问题的创新方法继续塑造数学领域，并对代数、分析和数论的发展产生了深远的影响。

　　问:阿贝尔在职业生涯中遇到过哪些挑战?

　　答:阿贝尔在他的职业生涯中面临着各种各样的挑战，包括经济困难，获得数学资源的机会有限，以及在他的一生中缺乏数学界的认可。尽管有这些障碍，他仍然坚持对数学知识的追求，并在该领域做出了重大贡献。

　　问:阿贝尔的工作对椭圆函数的研究有何影响?

　　A:阿贝尔在椭圆函数方面的工作为我们更深入地理解这些数学对象奠定了基础。他对椭圆函数性质和行为的研究为该领域的进一步发展铺平了道路，导致了复杂分析和代数几何等领域的进步。

　　问:今天亚伯的遗产有什么意义?

　　答:阿贝尔的遗产继续激励和影响着今天的数学家。他开创性的成果和开创性的解决问题的方法在数学领域留下了不可磨灭的印记。他发展的概念和理论仍然被研究和扩展，确保阿贝尔的贡献在现代数学中仍然具有相关性和影响力。